티스토리 뷰
728x90
[참고 출처] 고려대학교 한정현 교수님 연구실 강의자료 https://media.korea.ac.kr/books/
내적 (dot product): $a \cdot b$
- 두 개의 $n$ 차원 벡터
$a = (a_1, a_2, ..., a_n)$
$b = (b_1, b_2, ..., b_n)$ 일 때,
$a \cdot b = \sum^n_{t=1}a_ib_i = a_1b_1 + a_2b_2 + ... + a_nb_n$ - $a \cdot b = ||a|| \ ||b|| \cos{\theta}$
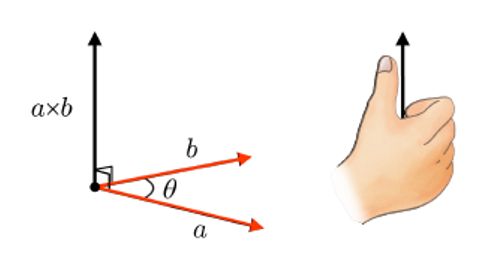
벡터곱 (cross product): $a \times b$
- 오른손 법칙을 따름.
- $|| a \times b || = ||a|| \ ||b|| \sin{\theta}$
- $a \times b$의 길이는 $a$와 $b$에 의해 만들어지는 평행사변형의 넓이와 같다.
- 두 벡터
$a = (a_x, a_y, a_z)$
$b = (b_x, b_y, b_z)$ 일 때,
$a \times b = (a_yb_z - a_zb_y, a_zb_x - a_xb_z, a_xb_y - a_yb_x)$ - $a \times b = - (a \times b)$
표준 기저를 구성하는 3개의 벡터 $e_1, e_2, e_3$ 간 상대적인 방향은 오른손 법칙에 따라 아래처럼 정의된다.
$e_1 \times e_2 = e_3$
$e_2 \times e_3 = e_1$
$e_3 \times e_1 = e_2$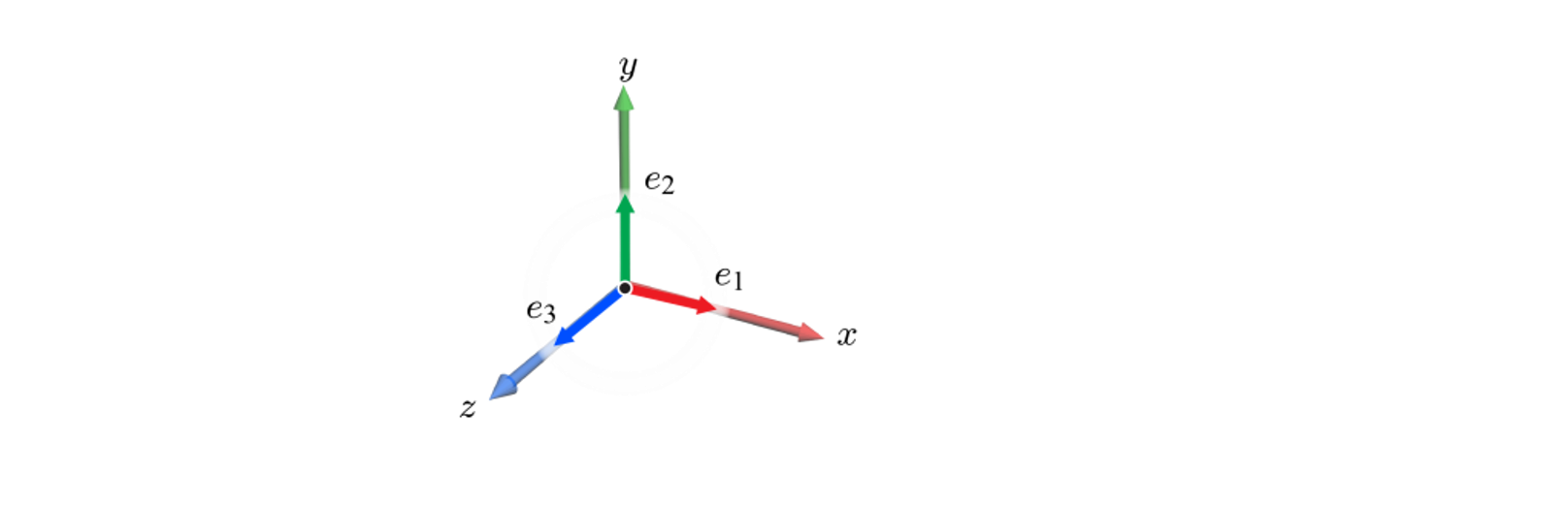
동일한 기저 벡터를 사용한 벡터곱 결과는 (0, 0, 0)이다.
$e_1 \times e_1 = e_2 \times e_2 = e_3 \times e_3 = 0$
직선 및 선형 보간(linear interpolation)

- 두 개의 점 $p_0$와 $p_1$을 지나는 직선은 $p_0$와, $p_0$와 $p_1$를 잇는 벡터 $p_1 - p_0$를 사용해 매개변수 방정식(parametric equation)으로 정의됨.
$p(t) = p_0 + t(p_1 - p_0)$ - 여기서 $t$는 $[-\infin, \infin]$ 범위에 놓이는 매개변수(parameter)이다.
- 만약 $t$의 범위가 $[0, \infin]$이라면, $p_0$에서 시작해서 $p_1 - p_0$ 방향으로 무한하게 뻗어나가는 광선(ray)가 됨.
- $(1-t)$ 와 $t$를 각각 $p_0$와 $p_1$에 대한 가중치(weight)로 보면,
$p(t)$는 $p_0$와 $p_1$의 가중치 합(weight sum)이 된다.
t가 0일수록 $p_0$에 가까워지고, t가 1일수록 $p_1$에 가까워지게 된다. - 특히, $t$의 범위가 $[0, 1]$일 때, $p(t)$는 $p_0$와 $p_1$의 선형보간(linear interpolation)이라고 한다.
- 함수 $p(t)$는 2차원 공간에서는 $(x(t), y(t))$, 3차원 공간에서는 $(x(t), y(t), z(t))$가 된다.
$p_0$와 $p_1$의 3차원 좌표를 각각 $(x_0, y_0, z_0)$와 $(x_1, y_1, z_1)$이라고 할 때, 각 좌표값에 선형보간을 적용해 $p(t)$의 좌표를 얻는다.
$p(t) = \begin{pmatrix}
x(t) \
y(t) \
z(t)
\end{pmatrix} =
\begin{pmatrix}
(1-t)x_0 + tx_1\
(1-t)y_0 + ty_1\
(1-t)z_0 + tz_1
\end{pmatrix}$ - 만약, $p_0$와 $p_1$에 특정한 값이 저장되어 있다면, 그 값들도 선형보간될 수 있다.
예를 들어, $p_0$에 $c_0$라는 색상이 저장되어 있고 그 원소를 $(R_0, G_0, B_0)$라 하자.
마찬가지로, $p_1$에 $c_1$이라는 색상이 저장되어 있고 그 원소를 $(R_1, G_1, B_1)$라 하자.
$RGB$ 원소 각각은 대개 [0, 255] 범위의 정수값, 혹은 [0, 1] 범위의 실수값을 가지는데,
선형보간된 색상 $c(t)$는 다음과 같이 정의된다.
$c(t) = (1-t)c_0 + tc_1 = \begin{pmatrix}
(1-t)R_0 + tR_1\
(1-t)G_0 + tG_1\
(1-t)B_0 + tB_1
\end{pmatrix}$
728x90
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- 브라우저
- 자료구조
- Python
- 함수
- Browser
- JavaScript
- useState
- 알고리즘
- leetcode
- zustand
- React Query
- 데이터베이스
- 자바스크립트
- error
- mdn
- 에러
- react
- github
- git
- 정렬
- 그래프
- BOJ
- 리액트
- Component
- CSS
- state
- Context API
- 파이썬
- DB
- DOM
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
글 보관함
250x250
