객체지향 프로그래밍 객체란? 자신의 상태를 가지며 역할을 수행하는 개체 객체 지향 프로그래밍이란? 프로그램을 명령어의 목록으로 보는 시각에서 벗어나, 여러 개의 독립된 단위인 객체들의 모임으로 파악하고자 하는 것이다. 각각의 객체는 메시지를 주고받고, 데이터를 처리할 수 있다. 객체 지향 프로그래밍은 프로그램을 유연하고 변경이 용이하게 만들기 때문에, 대규모 개발에 많이 사용된다. 객체 지향 프로그래밍 구현 방법 1. 객체를 기본적인 빌딩 블록으로 2. 각 객체는 어떤 타입(클래스)의 인스턴스 3. 클래스는 상속(inheritance)으로 연관 객체지향 프로그래밍의 특징 1. 캡슐화(Encapsulation) 💊 서로 관련있는 데이터와 함수를 객체 안에 하나로 묶고 외부에서 보일 필요가 없는 데이터를 잘..
 [문자열 검색] 한 살도 이해하는 KMP 알고리즘
[문자열 검색] 한 살도 이해하는 KMP 알고리즘
KMP 알고리즘이란? 대표적인 문자열 검색 알고리즘 KMP 알고리즘의 핵심 원리 문자열 매칭을 하면서 텍스트(전체 문자열)와 패턴(찾는 문자열)에서 서로 다른 글자가 나왔다면, '서로 다른 글자의 바로 전 까지는 일치했다'라는 사실과 '접두사와 접미사가 같은 만큼 비교를 덜해도 된다'는 사실 이용하기 즉, 바로 전 글자까지 일치했었으므로, 접미사와 접두사가 같은만큼 비교를 덜하도록 이동시켜주면 된다. 직접 하나하나 이해해보기 아래 그림을 보면서 이해해보자. @ @ @ @ a b c d a b c d @ @ @ @ 인 텍스트에서, (@는 아무 글자라고 생각하자, 신경안써도 된다.) a b c d a b c w z 인 패턴을 찾는다고 해보자. 첫 문자부터 하나 하나 비교를 시작한다. @ @ @ @ a b c..
 [벨만-포드 알고리즘] 한 살도 이해하는 벨만-포드 알고리즘(Bellman-Ford Algorithm)
[벨만-포드 알고리즘] 한 살도 이해하는 벨만-포드 알고리즘(Bellman-Ford Algorithm)
벨만-포드 알고리즘이란? 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다. 음의 가중치를 갖는 edge(간선)이 있을 때 사용하는 알고리즘이다. 다익스트라 알고리즘과 차이는 무엇인가? 다익스트라 알고리즘 - 매번 방문하지 않는 노드 중에서 최단거리가 가장 짧은 노드를 선택해 최단 거리를 구해나간다. - 음의 가중치를 갖는 edge(간선)이 없다면 최적의 해를 찾을 수 있다. - 시간 복잡도가 빠르다. 벨만-포드 알고리즘 - 매 단계마다 모든 edge(간선)을 전부 확인하면서 모든 노드간의 최단 거리를 구해나간다. - 음의 가중치를 갖는 edge가 있어도 최적의 해를 찾을 수 있다. - 시간 복잡도가 느리다. 즉, 모든 edge의 가중치가 양수일 때는 다익스트라 알고리즘을, 음의 가중치를 갖는..
 [다익스트라 알고리즘] 한 살도 이해하는 다익스트라 알고리즘
[다익스트라 알고리즘] 한 살도 이해하는 다익스트라 알고리즘
들어가기 전에 다익스트라 알고리즘을 이해하기 위해 여러 유튜브와 블로그를 방문했었는데 대체로 설명이 어렵거나 생략이 많다.. 코드 설명도 자세하지 않아 아쉬움이 있었다. (특히, 블로그에 있는 표나 그림은 왜이렇게 딱딱한걸까.. 잘 모르는 사람에겐 거부감이 든다) 직접 하나하나 그려가보며 이해한 나의 깨달음을 다른 분들께 자세하고 쉽게, 마치 아무것도 모르는 어린 아이에게 설명하듯이 설명해보려고 한다. 그리고 시간이 지나면 잊어버리는 미래의 나를 위하여 상세히 기술해보았다. 자세한 예시부터 점점 과정을 추상화해나가므로 이해하기 쉬울 것이라고 생각한다. 다익스트라 알고리즘이란? 그래프의 한 정점(Vertex 또는 Node)에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘으로, 최단 경로 문제에 사용된다..
 [탐색 트리] 한 살도 이해하는 B-트리
[탐색 트리] 한 살도 이해하는 B-트리
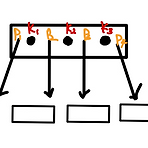
B-트리란? B-트리(B-tree)는 데이터베이스와 파일 시스템에 널리 사용되는 트리 자료구조의 일종으로, 이진 트리를 확장해 하나의 노드에 여러 개의 데이터를 저장한다. 차수가 p인 B-트리의 특성 1)적어도 노드의 반은 채워야 한다. 즉, root와 leaf를 제외한 모든 노드의 pointer 수 = 서브트리 수 = 최소 ⌈p / 2⌉개, 최대 p 개 2) root는 pointer를 2개 이상 가져야 한다. 즉, root의 서브트리의 수 >= 2 3) 모든 leaf는 같은 level (즉, 균형 트리이다) 4) 노드의 key 개수 leaf가 아닌 노드: pointer 수 - 1 개 = 서브트리 수 - 1개 (아래 B-트리 기본 구조 그림을 보면, key의 개수는 (pointer 개수 - 1)일 수 밖..
- Total
- Today
- Yesterday
- React Query
- CSS
- useState
- BOJ
- state
- leetcode
- 정렬
- JavaScript
- Context API
- git
- mdn
- github
- zustand
- 알고리즘
- 함수
- Python
- 리액트
- error
- 에러
- DB
- 자료구조
- react
- 자바스크립트
- Component
- 데이터베이스
- Browser
- 그래프
- 브라우저
- 파이썬
- DOM
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
